倒立摆的最优控制：LQR

发表于 2022-08-25 更新于 2022-10-08 分类于 Control

本文介绍如何利用线性二次调节器对最简单的单级倒立摆系统进行控制，使其保持倒立状态。

1. 什么是 LQR

LQR，全称 Linear-Quadratic Regulator，是最优控制中最基础的问题之一。其本质是对一个二次型的目标函数在一段时间内的总和/积分进行优化，从而得到最优的控制律。

将问题按照时间长度和系统是否为连续系统可以将 LQR 大致分为四类：1）无限时间长度，连续系统；2）无限时间长度，离散系统；3）有限时间长度，连续系统；4）有限时间长度，离散系统。以下文要使用的无限时间长度，离散系统为例，问题的数学描述为 ¹：

系统动力学方程：

\[ x_{k + 1} = {A} x_{k} + {B} u_{k} \] 要最小化的目标函数为： \[ J = \sum_{k=0}^{\infty} \left( x_k^T Q x_k + u_k^T R u_k + 2 x_k^T N u_k \right) \]

目标函数中的 \(Q\) 和 \(R\)，\(N\) 可以视为状态量和控制量大小的权重，且在大多数情况下，\(N\) 项通常是非必须的。

可以证明，使目标函数最小化的控制律为

\[ u_k = - F x_k \]

其中

\[ F = \left( R + B^T P B \right)^{-1} \left( B^T P A + N^T \right) \]

\(P\) 为 Riccati 方程的唯一正定解，满足方程

\[ P = A^T P A - \left(A^T P B \right) \left(R + B^T P B \right)^{-1} \left(B^T P A + N^T \right) + Q \]

利用以上的结论，就能用一个简单的反馈控制器 \(u_k = - F x_k\) 来实现对系统的最优控制。

2. 单级倒立摆系统的动力学描述

单级倒立摆系统的广义坐标定义如下图所示：

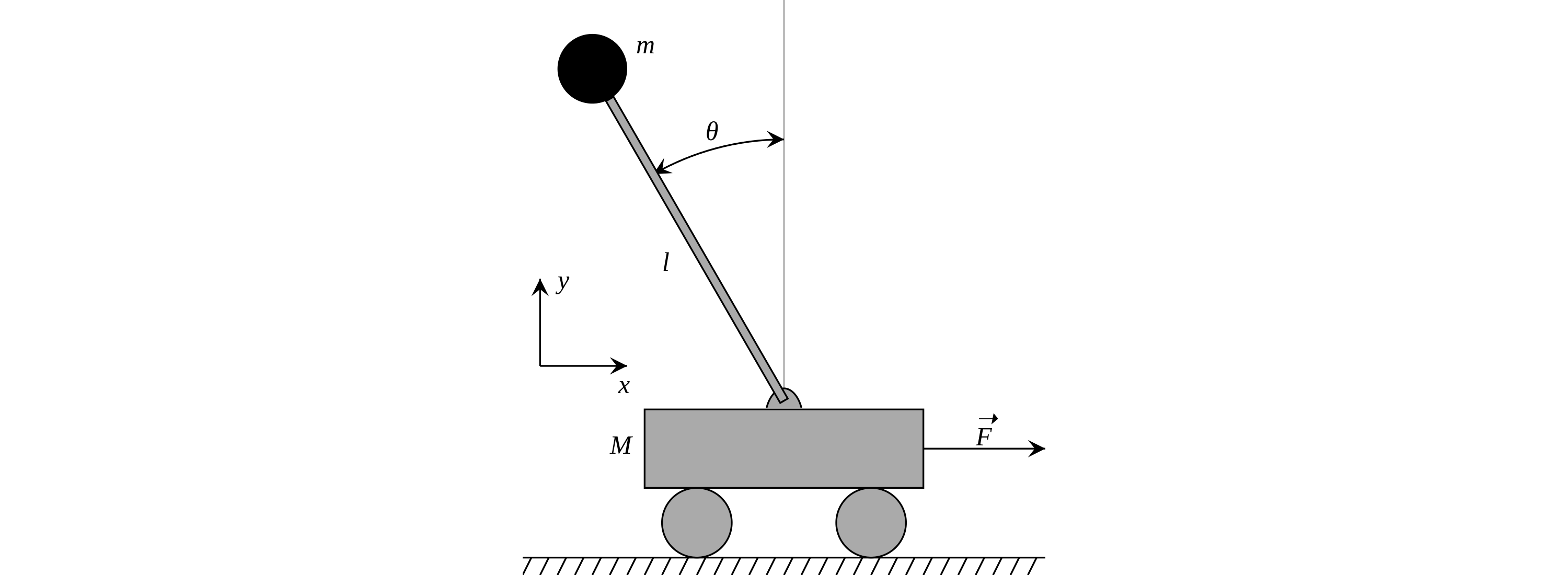
下面利用拉格朗日函数推导其动力学方程。

定义各变量分别为

小车质量：\(m_c\)

小球质量：\(m_p\)

杆长：\(l\)

杆与竖直方向夹角（逆时针为正）：\(\theta\)

小车水平方向位移（向右为正）：\(x\)

作用在小车上的力（向右为正）：\(u\)

重力加速度： \(g\)

系统的动能和势能分别为：

\[ V = m_p g l \cos\theta \]

\[ \begin{align} T &= \frac{1}{2} m_c \dot{x}^2 + \frac{1}{2}m_p \left[ (\dot{x} - l\dot{\theta}\cos{\theta})^2 + (l\dot{\theta} \sin{\theta})^2\right] \\ &= \frac{1}{2} (m_c + m_p) \dot{x}^2 + \frac{1}{2} m_p l^2 \dot{\theta}^2 - m_p l \dot{x}\dot{\theta}\cos{\theta} \end{align} \]

对应的拉格朗日函数为

\[ \begin{align} L &= T - V \\ &= \frac{1}{2} (m_c + m_p) \dot{x}^2 + \frac{1}{2} m_p l^2 \dot{\theta}^2 - m_p l \dot{x}\dot{\theta}\cos{\theta} - m_p g l \cos\theta \end{align} \]

根据以下方程

\[ \frac{d}{dt} \frac{\partial L}{\partial \dot{q}_i} - \frac{\partial L}{\partial q_i} = F_i \]

计算得到系统动力学方程为

\[ \begin{cases} \left( m_c + m_p \right) \ddot{x} - m_p l \ddot{\theta} \cos\theta + m_p l \dot{\theta}^2 \sin\theta = u\\ - m_p l \ddot{x} \cos\theta + m_p l^2 \ddot{\theta} - m_p g l \sin\theta = 0 \end{cases} \]

将以上方程写成矩阵形式，其中 \({q} = [x, \theta]^T\).

\[ {H(q)}{\ddot{q}} + {C(q, \dot{q})} {\dot{q}} + {G(q)} = {B} u \]

其中，各个矩阵为

\[ \begin{align} {H(q)} &= \begin{bmatrix} m_c + m_p & -m_p l \cos\theta \\ -m_p l \cos\theta & m_p l^2 \end{bmatrix} \\ {C(q, \dot{q})} &= \begin{bmatrix} 0 & m_p l \dot{\theta} \sin\theta \\ 0 & 0 \end{bmatrix} \\ {G(q)} &= \begin{bmatrix} 0 \\ -m_p g l \sin\theta \end{bmatrix} \\ {B} &= \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{align} \]

利用泰勒展开将上述动力学方程在零点附近展开，设系统状态变量为 \({x} = [x, \theta, \dot{x}, \dot{\theta}]^T\)，则线性化后的系统动力学方程为

\[ {\dot{x}} = {A_c} {x} + {B_c} u \]

其中各个矩阵为

\[ \begin{align} {A_c} &= \begin{bmatrix} {0} & {I} \\ -{H^{-1}} \frac{\partial {G}}{\partial {q}} & - {H^{-1}} {C} \end{bmatrix} \\ {B_c} &= \begin{bmatrix} {0}\\ {H^{-1}} {B} \end{bmatrix} \end{align} \]

得到上述动力学方程后就能利用各类现有的库计算最优的反馈增益 \({F}\)，下面给出利用 Matlab 的计算代码。由于在实际仿真中的计算是离散的，所以需要对上述的 \(A_c\)，\(B_c\) 矩阵做一定的变化，得到离散形式的控制方程。下面取仿真频率为 60Hz。

mp = 1.0;
mc = 1.0;
l = 1.0;
g = 9.81;
dt = 1 / 60.0;

H = [mc+ mp -mp*l;
    -mp*l mp*l^2];
b = [1;0];
dGdq = [0 0;0 -mp*g*l];

A = [zeros(2) eye(2);
    -H\dGdq zeros(2)];
B = [zeros(2,1); H\b];
Q = diag([10 10 0 0]);
R = 1;

[F, S, e] = dlqr(A * dt + eye(4), B * dt, Q, R);
disp(F);

计算得到

1 2	F = -2.8999 58.2537 -4.8034 15.2054

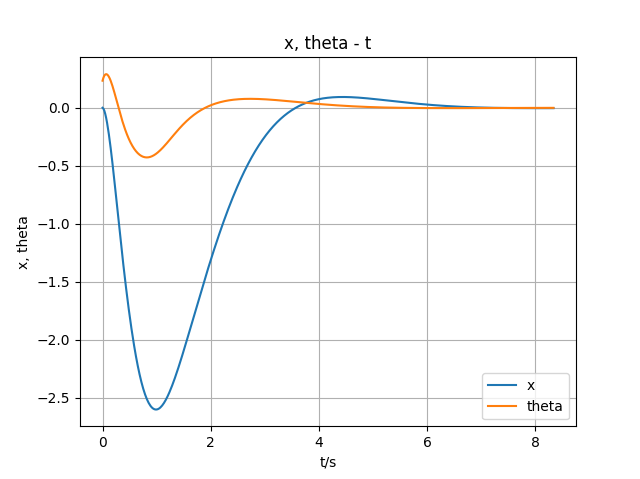
在 isaacgym 中进行仿真

状态量随时间变化如下图所示

维基百科——LQR 控制器：https://zh.wikipedia.org/zh-cn/LQR%E6%8E%A7%E5%88%B6%E5%99%A8↩︎