Pytorch 中的计算图及其可视化

发表于 更新于 分类于

前一段时间在复现 PPO 算法的时候出了 bug 找不到问题所在，所以想检查一下各个张量在 Pytorch 中的反向传播是否正确。这篇文章把当时阅读的一些关于 Pytorch 自动梯度计算的资料做一个总结，主要介绍 Pytorch 中的自动梯度计算原理及其反向传播路径的可视化。代码层面的实现不做展开。

1. Pytorch 的自动梯度计算

在 Pytorch 中，对神经网络参数的优化的关键步骤往往包含几个部分：优化器的选择；损失函数的计算；以及根据损失函数计算梯度，反向传播更新梯度。以我在复现的代码为例子，上述几个步骤对应的核心代码为：

1
2
3
4
5
6
7
8
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

# calculate a scalar loss related to the parameters of the model
loss = ...

optimizer.zero_grad()
loss.backward()
optimizer.step()

对不了解 Pytorch 底层反向传播过程中自动梯度计算过程的人来说，上述代码中的后三行会引发一系列的疑问：为什么给定一个标量形式的 loss 就能实现梯度的计算；为什么在计算梯度前需要调用 optimizer.zero_grad() 这个方法；能不能调用多次 loss.backward()； optimizer.step() 的过程中到底发生了什么？本篇文章意在介绍自动梯度计算的原理和一些基础的技术实现，以及简单说明在上述过程中，Pytorch 干了什么。

1.1. 求导的链式法则

在数学层面上，反向梯度计算涉及到链式法则。这里给出一个简单的例子：

\[ \begin{align} & \text{Define input tensor: } a\\ & \text{Define parameters: } w_1, w_2\\ & b = a * w_1\\ & c = b + w_2\\ & d = b * c\\ \end{align} \]

则运算结果 d 关于输入 a 的梯度计算可以表示为：

\[ \begin{split} &\frac{\partial d}{\partial a}\\ =& \frac{\partial d}{\partial c} \frac{\partial c}{\partial a} + \frac{\partial d}{\partial b}\frac{\partial b}{\partial a}\\ =& \frac{\partial d}{\partial c} \frac{\partial c}{\partial b} \frac{\partial b}{\partial a} + \frac{\partial d}{\partial b}\frac{\partial b}{\partial a}\\ =& w_1^2 a + w_1 w_2 a + w_2^2 \end{split} \]

从上述过程中可以看到，梯度计算的过程就是利用链式法则从最后一步开始，反向计算各个中间变量（如 b，c）的梯度。对该过程进行抽象，则如果我们知道以下的信息，就能根据链式法则计算梯度：1）输入；2）每一步计算中，使用的函数对应的导数的表达式；3）各步计算之间的顺序关系。在 Pytorch 中，利用“图”这一种数据结构对各步计算的顺序关系进行描述。

1.2. Pytorch 的计算图

根据维基百科，关于图数据结构的描述为：

图（英语：graph）是一种抽象数据类型，用于实现数学中图论的无向图和有向图的概念。图的数据结构包含一个有限（可能是可变的）的集合作为节点集合，以及一个无序对（对应无向图）或有序对（对应有向图）的集合作为边（有向图中也称作弧）的集合。节点可以是图结构的一部分，也可以是用整数下标或引用表示的外部实体。图的数据结构还可能包含和每条边相关联的数值（edge value），例如一个标号或一个数值（即权重，weight；表示花费、容量、长度等）。

对自动梯度计算来说，图中的节点表示各个运算和张量，边表示各个张量之间的顺序关系，如 1.1 的例子可以用下面一张图进行表示：

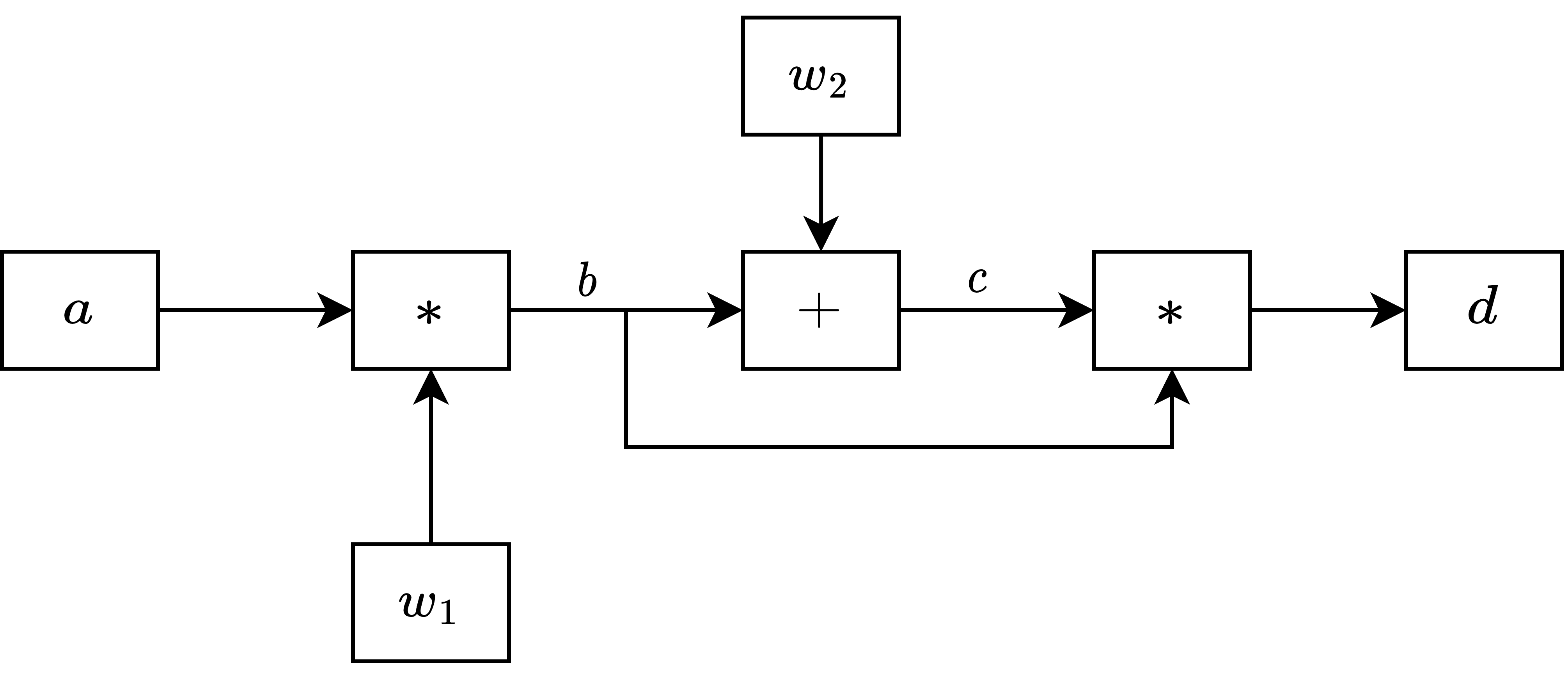
对于仅含加法和乘法的计算图，运算结果 d 关于输入 a 的梯度计算可以表示为上述路径从输出到输入各条路径的梯度累乘的和。如在上图中，从输出到输入共有两条路径：1）a -> * -> b -> * -> d 和 ；2）a -> * -> b -> + -> c -> * -> d。

第一条路径的梯度累乘为：

\[ \frac{\partial d}{\partial b} \frac{\partial b}{\partial a} \]

第二条路径的梯度累乘为：

\[ \frac{\partial d}{\partial c} \frac{\partial c}{\partial b} \frac{\partial b}{\partial a} \]

则两条路径的和即为输出关于输入的梯度：

\[ \begin{split} &\frac{\partial d}{\partial a}\\ =& \frac{\partial d}{\partial c} \frac{\partial c}{\partial a} + \frac{\partial d}{\partial b}\frac{\partial b}{\partial a}\\ =& \frac{\partial d}{\partial c} \frac{\partial c}{\partial b} \frac{\partial b}{\partial a} + \frac{\partial d}{\partial b}\frac{\partial b}{\partial a}\\ \end{split} \]

对于更一般的计算图，可能包含加法和乘法之外的运算，此时不能通过简单的对各条路径的梯度累乘求和来得到输出关于输入的梯度。在 Pytorch 中，提供了 Function 类用于自定义运算，使用者需要定义 forward() 和 backward() 这两个类方法来供 Pytorch 调用，以实现自动梯度计算。在 Pytorch 中，已经实现了大多数常用运算对应的 Function 类，因此在使用过程中一般直接对张量进行计算， Pytorch 就会自动生成计算图，实现自动梯度计算。

1.3. Pytorch 代码的每一步的作用

这里简单说明上述的核心代码的例子中，每一步对应着 Pytorch 的什么行为。这里再把代码贴一遍：

1
2
3
4
5
6
7
8
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

# calculate a scalar loss related to the parameters of the model
loss = ...

optimizer.zero_grad()
loss.backward()
optimizer.step()

首先，定义优化器 optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate) 该优化器会根据各个可训练参数张量（model.parameters()）对应的梯度，来更新这些可训练参数张量的值，该优化过程通过调用 optimizer.step() 实现。

定义完成优化器后，根据具体任务定义损失函数。损失函数必须是各个可训练参数张量的函数，这样，进行自动梯度计算时，才能正确地将梯度信息反向传播到可训练参数张量。

计算得到损失函数后，在进行自动梯度计算之前，必须利用 optimizer.zero_grad() 先将各个张量现有的梯度全部置零。这是因为 Pytorch 在每次 backward() 之后，都会将新的梯度信息累加到现有的梯度信息上，而不是覆盖掉现有的梯度信息。

然后就是以损失函数为输出量，各个训练参数张量为输入量，计算梯度。该步对应 loss.backward()。需要注意的是，进行 backward 后，如果没有设置额外的 retain_graph 参数，计算图就会被销毁，此时就不能进行第二次 backward 了。也正如上一段中提到的，如果设置了 retain_graph=True 且进行了第二次 backward，则梯度会变成只进行一次 backward 的两倍。

最后让优化器利用梯度对各个张量的值进行更新： optmizer.step()。

2. Pytorch 反向传播路径的可视化

知道了 Pytorch 是如何实现反向传播的之后，想单纯通过现代 IDE 的 debug 功能来获取计算图仍然是一件比较麻烦的事情，一个自然的想法就是调用一些现有的库来实现计算图的可视化。根据我的调研，Pytorch 相关的实现图可视化功能的有 Tensorboard 的 add_graph() 函数 和一个可视化工具 pytorchviz。 其中，add_graph() 函数仅适用于 torch.nn.Module 的子类，且该子类必须定义 forward() 函数，而不能获取全局的计算图。而 pytorchviz 能够从某一个张量开始，获得其所有上游节点构成的计算图。

以 pytorchviz github 库中的例子对其使用进行说明， 实例代码 如下：

1
2
3
4
5
6
7
8
9
model = nn.Sequential()
model.add_module('W0', nn.Linear(8, 16))
model.add_module('tanh', nn.Tanh())
model.add_module('W1', nn.Linear(16, 1))

x = torch.randn(1, 8)
y = model(x)

make_dot(y.mean(), params=dict(model.named_parameters()))

首先创建一个网络模型 model，然后给定输入 x ，计算得到输出 y，然后对输出 y 取平均得到一个标量 y.mean()（ Pytorch 只支持对标量形式的数据进行自动梯度计算），调用 pytorchviz 库中的 make_dot 函数可以得到一个 dot 对象，然后进行后续的处理来得到可视化的计算图，如下所示

1
2
dot = make_dot(y.mean(), params=dict(model.named_parameters()))
dot.render(filename="backward_graph", directory=log_dir, format="pdf")

上述代码会将 dot 对象渲染成 pdf 格式的文件，并存储到 log_dir 文件夹。需要注意的是，渲染需要 graphviz 的支持，在 ubuntu 系统下，可以简单地通过命令行进行安装。

1
$ sudo apt install graphviz

其他系统的安装可以参考 graphviz 的官方文档

在文章最后会给出我在 debug PPO 算法时，渲染得到的计算图。

3. 一些参考链接

这篇文章介绍得相当简略，由于我的本意是对计算图进行可视化来 debug，而不是从底层开始了解自动梯度计算的全过程，所以很多关于 Pytorch 自动梯度计算的实现和 pytorchviz 的内部原理都没有做深入了解，这里给出一些参考的链接。

关于 Pytorch 中张量、计算图、张量运算的入门介绍，可以参考 PyTorch 101 系列文章，这是其中 第一篇的链接。

关于自动梯度计算的代码实现， Pytorch 官方文档 和 一篇介绍 backward 过程的知乎文章 有更为详细的介绍。

关于 pytorchviz 这个工具的实现原理，stackoverflow 上有一个 相关性比较高的回答 可以作参考。

附录：PPO 对应的计算图