变分自编码器：Variational Autoencoder

发表于 2023-03-03 更新于 2023-04-26 分类于 Unsurpervised Learning

关于变分自编码器（Variational Autoencoder，VAE）的一些基础理论。

变分自编码器（VAE）是基于有向概率图模型的一种生成模型，其目标通常是进行极大似然估计（maximize likelihood）和最大化后验分布（maximize a posterior）。从结构上来看，它包含编码器（encoder）和解码器（decoder）两个部分：编码器负责将数据点映射到特征空间，解码器则负责将上一步得到的特征向量映射回数据点，最终实现基于特征向量的数据重建。

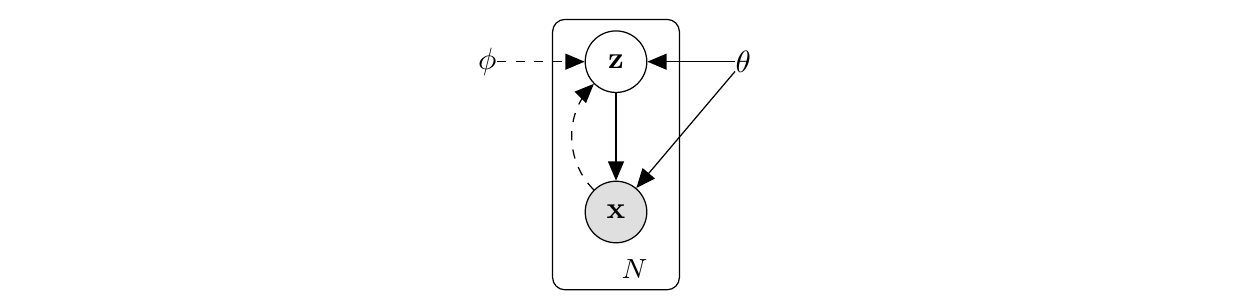
VAE 对数据的假设及一些表示

一些假设及表示
- 假设
  - dataset \(X = {x^{(i)}}^N_{i=1}\)
  - dataset 满足独立同分布，生成过程包含隐变量 \(z\)
  - 数据生成过程
    - 根据先验 \(p_{\theta^\star} (z)\) 生成特征向量 \(z\)
    - 根据特征向量，从条件分布 \(p_{\theta^\star} (x|z)\) 生成数据 \(x\)
    - 假设上述的先验和条件分布对特征向量 \(z\) 和数据 \(x\) 是可微的
- 表示
  - 生成模型：\(p_\theta(z) p_\theta (x|z)\)
  - 对隐变量的变分后验估计 \(q_\phi (z| x)\)

最大似然情况下的 VAE 理论推导

\[ \begin{split} \log {p_\theta (x^{i})} &= \mathbb{E}_{q_\phi (z|x^{i})} \left[ \log p_\theta (x^{i}) \right] \\ &= \mathbb{E}_{q_\phi (z|x^{i})} \left[ \log p_\theta (x^{i}, z) - \log p_\theta (z | x^{i}) \right] \\ &= \mathbb{E}_{q_\phi (z|x^{i})} \left[ \log p_\theta (x^{i}, z) - \log p_\theta (z | x^{i}) + \log q_\phi (z|x^{i}) - \log q_\phi (z|x^{i}) \right] \\ &= \mathbb{E}_{q_\phi (z|x^{i})} \left[ \log q_\phi (z|x^{i}) - \log p_\theta (z | x^{i}) - \log q_\phi (z|x^{i}) + \log p_\theta (x^{i}, z) \right] \\ &\equiv D_{KL} (q_\phi (z|x^{i}) || p_\theta (z | x^{i})) + \mathcal{L}(\theta, \phi; x^{(i)}) \end{split} \]

上式中的 \(\mathcal{L}\) 的定义为

\[ \mathcal{L}(\theta, \phi; x^{(i)}) = \mathbb{E}_{q_\phi (z|x^{i})} \left[ - \log q_\phi (z|x^{i}) + \log p_\theta (x^{i}, z) \right] \tag{form 1} \]

其也能表示为以下的形式

\[ \mathcal{L}(\theta, \phi; x^{(i)}) = -D_{KL}(q_\phi (z|x^{(i)}) || p_\theta (z)) + \mathbb{E}_{q_\phi (z|x^{i})} \left[ \log p_\theta (x^{(i)}|z) \right] \tag{form 2} \]

由于 KL 散度恒大于 0 ，因此 \(\mathcal{L}\) 也是最大似然函数 \(\log {p_\theta (x^{i})}\) 的一个下界。

要对上述下界进行优化，往往需要对该下界的梯度进行估计。利用 reparameterize 的技巧，上述两种变分下界的表达形式能够分别得到一种 estimator。在给出两种估计器的形式前，首先介绍 reparameterize 方法。

Reparameterization

引入 reparameterization 是为了能够对变分估计 \(\mathcal{L}(\theta, \phi; x^{(i)})\) 及其导数进行计算或估计。 reparameterization 最核心的想法，就是使用一个确定性的含噪声的函数（因此可以直接进行微分）取代原有的概率分布，对于特征向量 \(z\)，其条件后验分布满足 \(z \sim q_\phi (z|x)\)。通过引入函数

\[ z = g_\phi (\epsilon, x), \quad \epsilon \sim p(\epsilon) \]

则对任意与 \(z\) 相关的随机变量在 \(q_\phi(z|x)\) 分布下的期望可以重写为

\[ \begin{split} & \mathbb{E}_{q_\phi(z|x)} f(z) \\ =& \int q_\phi (z|x) f(z) dz \\ =& \int p(\epsilon) f(z) d\epsilon\\ =& \int p(\epsilon) f(g_\phi(\epsilon, x)) d\epsilon \end{split} \]

对 ELBO 的可微估计

利用 reparameterize 的方法，能够得到对 \(f(z)\) 的可微估计

\[ \int p(\epsilon) f(z) d\epsilon = \frac{1}{L} \sum_{l = 1}^{L} f(g_\phi(\epsilon^{l}, x)) \]

上述估计是关于参数 \(\phi\) 的函数，因此可以对 \(\phi\) 进行微分，从而得到其导数。

Stochasitic Gradient Variational Bayes (SGVB)

根据变分下界的两种形式，结合 reparameterize 方法，能够得到两种变分下界的估计

\[ \begin{align} & \hat{\mathcal{L}}^A (\theta, \phi; x^{(i)}) = \frac{1}{L} \sum_{l = 1}^L \log p_\theta (x^{(i)}, z^{(i, l)}) - \log q_\phi (z^{(i, l)}|x^{(i)})\\ & \text{where} \,\, z^{(i, l)} = g_\phi (\epsilon^{(i, l)}, x^{(i)}), \,\, \text{and} \,\, \epsilon^{(i)} \sim p(\epsilon) \end{align} \tag{SGVB form 1} \] \[ \begin{align} & \hat{\mathcal{L}}^B (\theta, \phi; x^{(i)}) = - D_{KL} (q_\phi (z|x^{(i)}) || p_\theta (z)) + \frac{1}{L} \sum_{l = 1}^{L} (\log p_\theta (x^{(i)}|z^{(i, l)}))\\ & \text{where} \,\, z^{(i, l)} = g_\phi (\epsilon^{(i, l)}, x^{(i)}), \,\, \text{and} \,\, \epsilon^{(i)} \sim p(\epsilon) \end{align} \tag{SGVB form 2} \]

VAE 的训练

对变分下界的值及其导数进行估计后，通过优化使得变分下界达到最大，就能实现对 VAE 的训练。需要注意的是，大多数现有的优化器默认都是向着目标函数最小的方向进行优化的，在具体实现时要注意优化目标是否也是最小化。

除了基础了理论推导外，原文还给出了针对高斯分布先验 \(p(z)\) 和多变量高斯分布后验 \(q(z|x)\) 的变分自编码器的训练损失函数，该损失函数也是各个库中 vanilla VAE 所使用的损失函数。